Con ligeros cambios a las matrices, se pueden combinar para conseguir que una sola matriz resultante nos sirva para varias de estas transformaciones
MÉTODO DE TRASLACIÓN
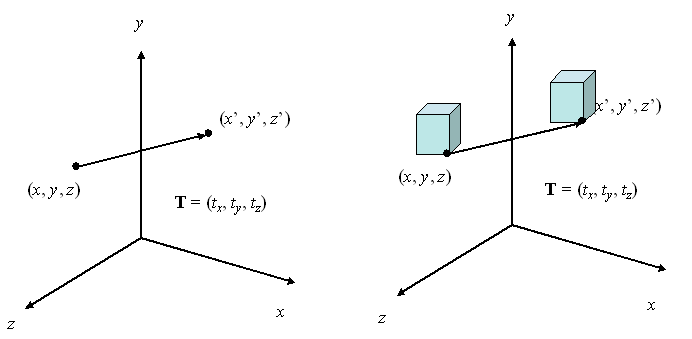
En una representación coordenada homogénea
tridimensional, un punto es trasladado (fig.11.1) de la posición (x,y,z) a la posición (x’,y’,z’)
con la Operación
matricial.
[x´,y´,z´,1]=[x, y, z, 1]
(11.1)
Los parámetros Tx,
Ty, Tz, que especifican distancias de traslación para las coordenadas,
reciben la asignación de cualquier valor
real. La representación matricial de la ecuación 11.1 es equivalente a las tres
ecuaciones
x’ =x
+ Tx, y’ = y + Ty, z’ =z + Tz
Un objetivo se traslada en tres dimensiones
transformando cada punto definidor del objeto. La traslación de un objeto
representada como un conjunto de superficies poligonales se efectúa trasladando
los valores coordenados para cada vértice de cada superficie. El conjunto de
posiciones coordenadas trasladadas de los vértices define entonces la nueva
posición del objeto.
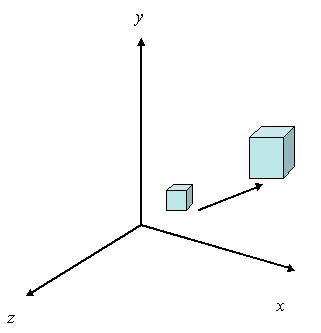
MÉTODO DE ESCALACIÓN
Operación matricial.
[x´,y´,z´,1]=[x, y, z, 1]
Los parámetros de escalación Sx, Sy,
Sz, se les asigna asignación cualquier valor positivo.
Cuando la
transformación 11-3 se aplica para definir puntos en un objeto, el objeto se
escala y se desplaza en relación con el origen coordenado.
MÉTODO DE ROTACIÓN
Para especificar una transformación de rotación de
un objeto, se debe designar un eje de rotación (en torno al cual se hará girar
el objeto) y la cantidad de rotación angular. En aplicaciones bidimensionales,
el eje de rotación siempre es perpendicular al plano xy. En tres dimensiones,
un eje de rotación puede tener cualquier orientación espacial.los ejes de
rotación más fáciles de manejar son aquellos que son paralelos a los ejes
coordenados. Asimismo, podemos valernos de las rotaciones en torno a los tres
ejes coordenados con el fin de producir una rotación en torno a cualquier eje
de rotación especificado en forma arbitraria.
Las direcciones de rotación positivas en torno a los
ejes coordenados son en sentido contrario al del reloj, como se observa a lo
largo de la posición positiva de cada eje en dirección del origen.
Operación matricial de rotación en el eje Z
El parámetro Ѳ especifica el ángulo de rotación.
[x´,y´,z´,1]=[x, y, z, 1]
Imagen que muestra la rotación de un objeto en torno
al eje Z.
Operación matricial de rotación en el eje X
[x´,y´,z´,1]=[x, y, z, 1]
Operación matricial de rotación en el eje y
[x´,y´,z´,1]=[x, y, z, 1]


No hay comentarios:
Publicar un comentario